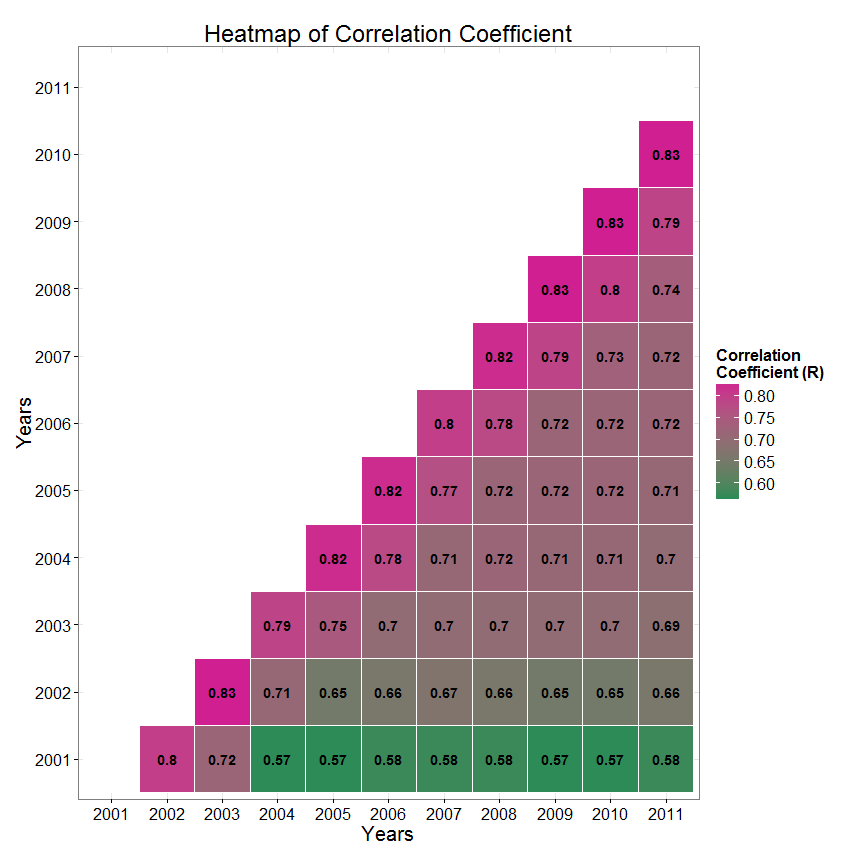
Tout est partis de la rédaction d'un article pour une revue de télédétection dans laquelle j'avais une matrice de corrélation à partir d'un raster multibandes à présenter! Bon une matrice de corrélation c'est pas franchement "sexy" à présenter donc je me suis dit que je pouvais grâce à R et toutes les possibilités qu'il offre réussir à faire quelque chose qui change de l'ordinaire!
Dans mon cas, il s'agissait de vérifier la non-stabilité (c'est à dire la potentielle dynamique) du domaine cultivé en Afrique de l'Ouest à partir du produit MODIS land Cover! Initialement j'ai donc une image avec 11 bandes binaires (culture / non culture, entre 2001 et 2011), présentées ci dessous:
Voici donc la démarche que j'ai suivi :
########################################
# Initialisation de l'espace de travail
setwd("D:/MyFolder")
#Packages nécéssaires
library(raster)
library(sp)
library(Hmisc)
library(plyr)
library(reshape2)
library(ggplot2)
#############Importation des données raster et stockage des bandes dans une matrice#######
filename<-'mon_image.tif'# variable stockant le nom du fichier
nband<-nbands(raster(filename)) #variable stockant le nombre de bandes dans l'image
cell<-ncell(raster(filename)) #variable stockant le nombre de pixel d'une bande
mat<-matrix(0, ncol=nband, nrow=cell) #initialisation de la matrice reçevant les valeurs des bandes de l'image
for (i in 1:nband){
mat[,i]<-getValues(raster(filename, band=i))
}
#############Création de la matrice de corrélation#######
cor<-rcorr(mat,type="pearson") # création de la matrice de corrélation
coef.corr<-cor$r # récupère la matrice de coefficients de corrélation
#############Mise en forme de la matrice de corrélation pour la création du graphique#######
coef.corr[coef.corr==1]<-0 #valeurs de la diagonale mises à 0
# Boucle garder que la première moitié du tableau de corrélation (éviter la duplication dans le graphique)
for (i in 1:nband){
for (j in 1:nband){
if (coef.corr[i,j]==0){
coef.corr[i:nband,j]<- 0
}
}
}
coef.corr[coef.corr==0]<-NA
mat.m<-melt(coef.corr, na.rm=FALSE)
mat.n<-ddply(mat.m, .(Var1), transform)
r<-round(mat.n$value,2) #arrondissement des coefficients de corrélation à deux chiffres après la virgule
mat.r<-cbind(mat.n[,1:2],r)
#############Diagramme à deux dimensions avec ggplot2#######
labelsx<-seq(2001,2011,1) #noms de l'axe des x
labelsy<-seq(2001,2011,1) #noms de l'axe des y
#Graphique
ggplot(mat.r, aes(factor(Var1), factor(Var2), label=r))+ geom_tile(aes(fill=r ),colour="white")+scale_fill_gradient(low="seagreen4", high="violetred", na.value="white")+geom_text(aes(fontface=2))+ylab("Years")+xlab("Years")+labs(fill="Correlation \nCoefficient (R)")+labs(title="Heatmap of Correlation Coefficient")+theme(axis.title.x=element_text(size=20), axis.title.y=element_text(size=20),axis.text.x=element_text(size=10), axis.text.y=element_text(size=10),plot.title=element_text(size=20))+theme_bw(base_size=20, base_family=2)+scale_x_discrete(labels=labelsx)+scale_y_discrete(labels=labelsy)+coord_flip()
########################################
Et voilà, vous obtiendrez un chouette graphique que celui-ci:

3 août 2017 — 16 h 41 min
Ce code m’a beaucoup aider merci pour le partage !
30 août 2017 — 13 h 19 min
Merci pour votre retour, je fais passer le message à Louise